全面的分析和强大的统计能力,一切易如反掌
有效组织您的数据
Prism为您的分析进行了特别的设计 -- 定量分析和分类数据分析。使得正确输入数据、选择合适的分析和创建精美的图表变得更加容易。
进行正确的分析
避免使用统计术语。Prism使用清晰的语言提供大量的分析库,涵盖从普通到高度特定的分析 — 包括非线性回归、t检验、非参数比较、方差分析(单因素、双因素和三因素)、列联表分析、生存分析等等。每项分析都列有一个清单,以帮助您了解所需的统计假设并确认您选择了适当的检验。
随时获得可操作的帮助
降低统计数据的复杂性。GraphPad Prism的在线帮助超出了你的预期。在几乎每一步,您都可以访问数千页的Prism用户指南;并可以通过Prism Academy学习视频课程、指南和培训材料,浏览图形组合并学习如何制作各种图形类型。同时,GraphPad为您提供了教程数据集,可以帮助您理解为什么应该执行某些分析以及如何解释结果。

巧干,而不是苦干

一键式回归分析
没有其他程序能像Prism那样简化曲线拟合。 选择方程式,Prism即可完成其余工作 - 拟合曲线、显示结果和函数参数列表,在图形上绘制曲线并插入未知值。
专注于研究而不是软件
无需编码。 图形和结果会实时自动更新。 数据和分析的任何更改(添加丢失的数据、省略错误的数据、纠正错别字或更改分析选择)都将立即反映在结果、图形和布局中。
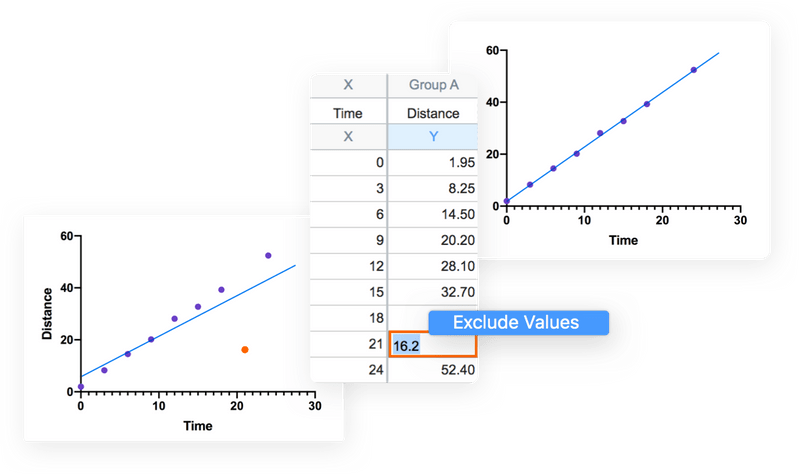
无需编程即可让您的工作自动执行
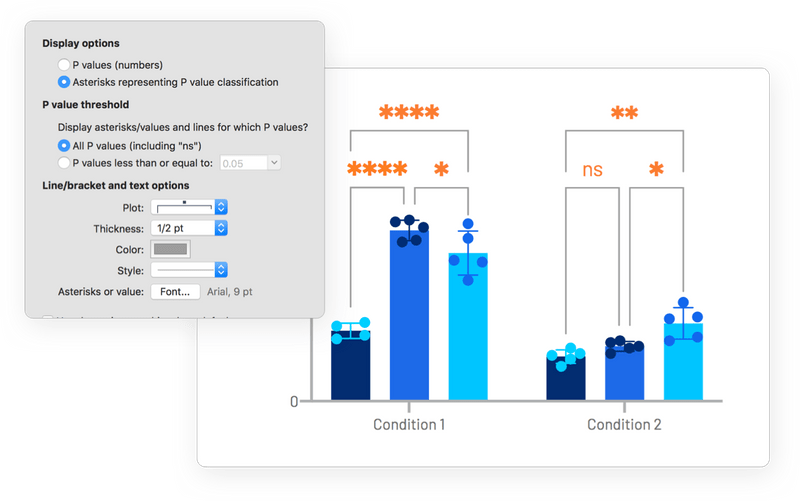
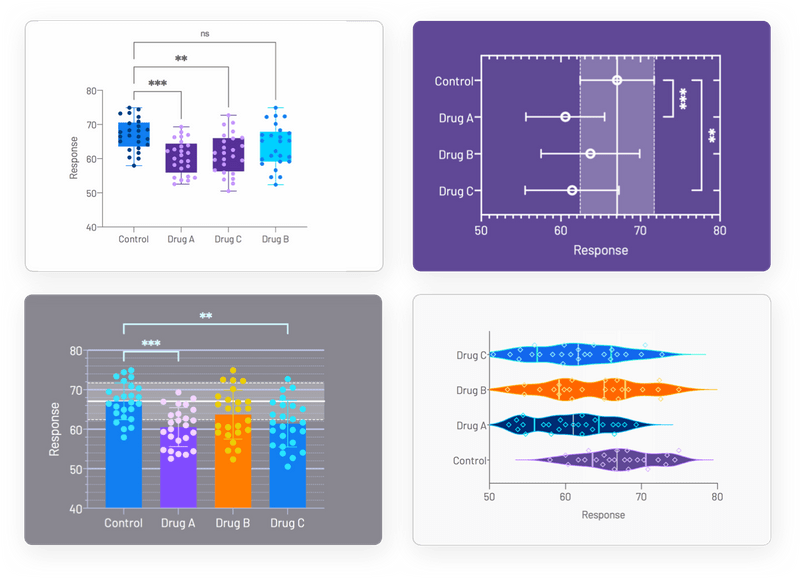
只需点击一下,即可自动将多个成对比较添加到您的分析中。只需点击工具栏按钮,即可执行这些线和星号的自定义选项。对数据或分析进行的调整,图上显示的分析结果也将自动更新。
优美绘图和分享工作成果的最快方法
众多的自定义图形方法
更直观地展示您的数据,而不是操作软件。 Prism让创建所需的图形变得容易。 选择图形类型,然后自定义任何部分 - 数据的排列方式、数据点的样式、标签、字体、颜色等等。 自定义选项不尽其数。
探索你的数据
让您集中精力分析最相关的数据。您可自定义如何在数据中表示关系,以有效地探索大量数据集。您在这里注意到有趣的事情了吗?突出显示单个数据点以探索其相应的属性。利用prism强大的数据整理功能,您既可以节省时间,又可以确保您的分析基于干净且结构良好的数据。
一键导出出版质量的图形
减少发表所需的时间。 Prism允许您自定义导出(文件类型、分辨率、透明度、尺寸、色彩空间 RGB/CMYK),以满足期刊的要求。 设置默认值以节省时间。
加强协作
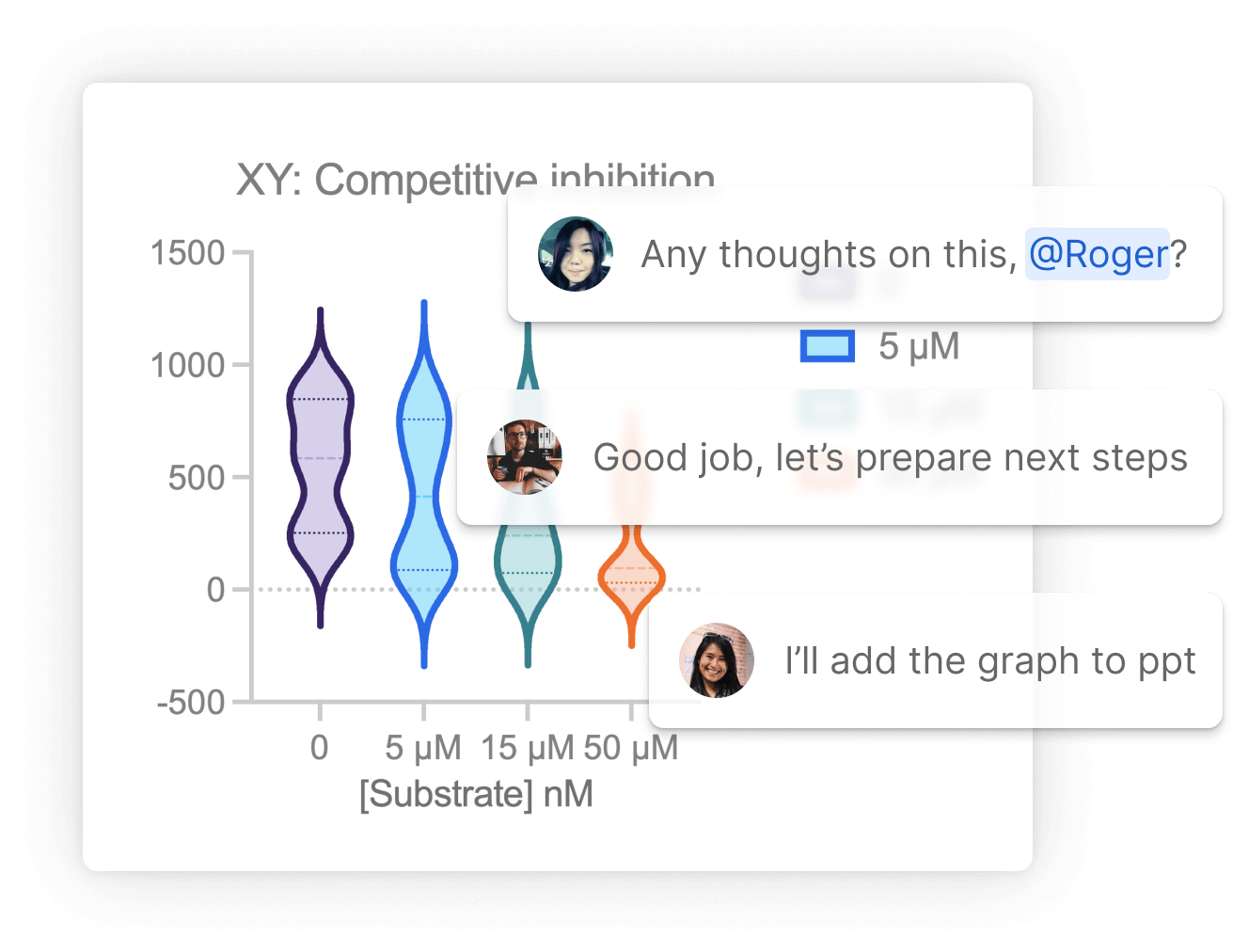
不仅限于分享您的图表。 Prism全面记录您的数据,使您能够与其他科学家有效进行协作。 Prism项目的所有部分(原始数据、分析、结果、图形和布局)都包含在一个单一的文件中,一次单击即可完成共享。 这样,其他人就可以轻松同步您的工作,从而提高了结果的清晰度并简化了协作过程。
探索GraphPad Prism 10的新功能!
隆重推出功能更强大的Prism,它具有增强的数据可视化和图形自定义能力,可进行更直观的导航和更复杂的统计分析。
增强的数据可视化功能
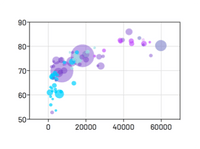
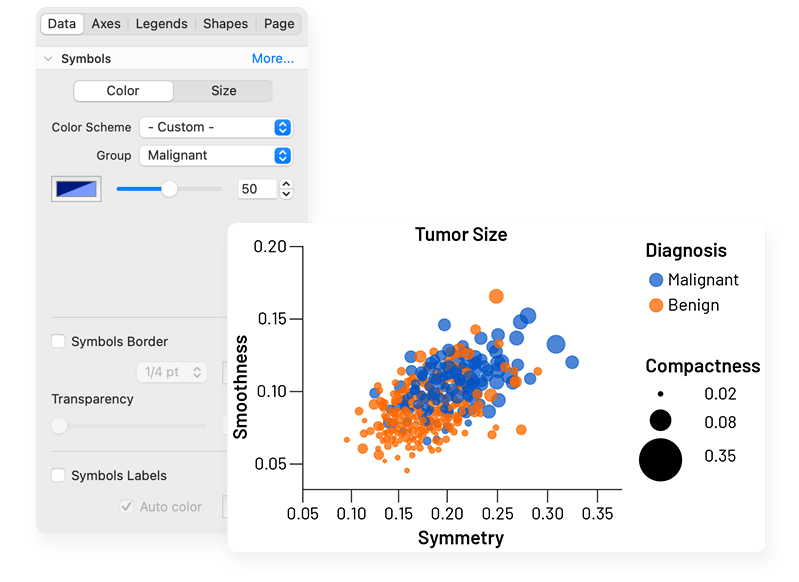
气泡图
直接通过表示位置(x和y坐标)、颜色和尺寸变量的原始数据即可创建气泡图
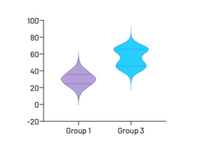
小提琴图
与箱线图或简单的条形图相比,小提琴图可更清晰地显示大数据集的分布
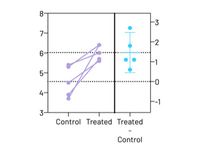
估计图
自动显示您的分析结果
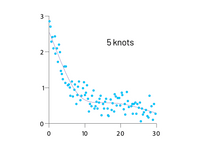
平滑样条
重大改进是在于通过 Akima 样条和平滑样条显示一般数据的趋势,并改进了对节点或拐点数量的控制
增强的制图和自定义选项
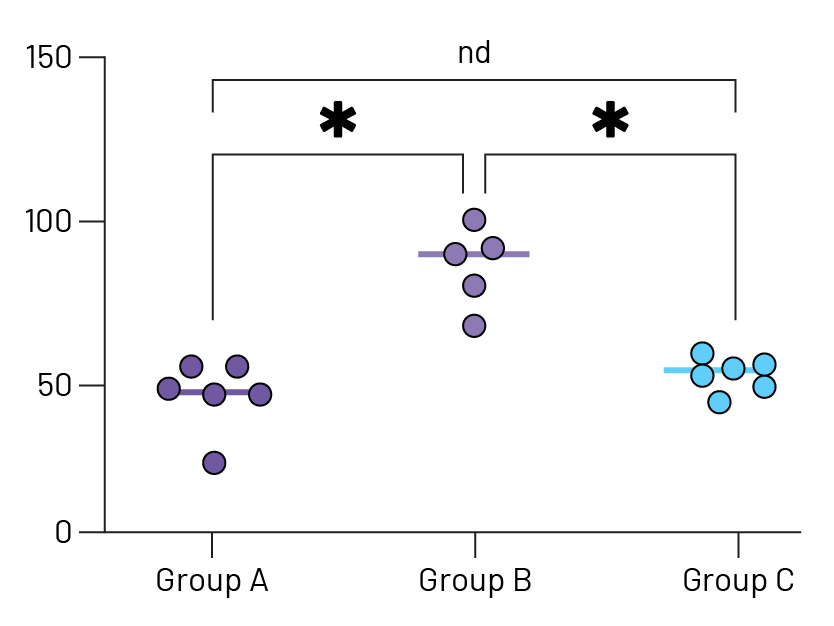
图形上的星号
自动添加多个比较结果到图表。可从各种P值摘要样式中进行选择,包括适用于任何alpha水平的响应方法。
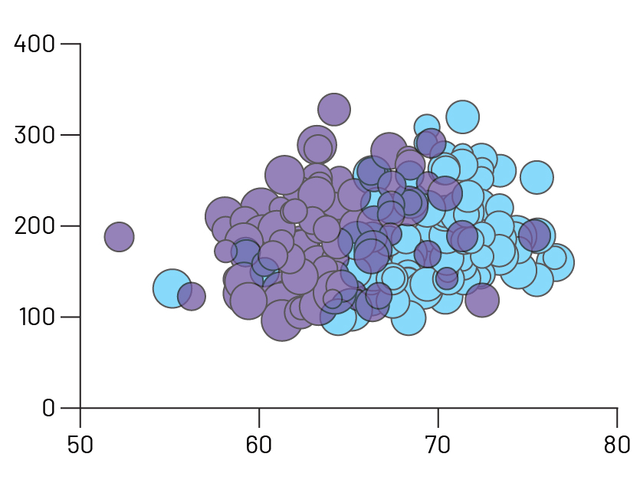
改进的图形自定义设置
比以前更快、更容易、更直观地绘制出令人惊叹的气泡图。实时交互和自定义多变量数据中的图表。
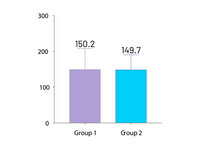
自动标注条形图
在柱状图上标注均值、中位数或样本量,以强调您工作的重点。
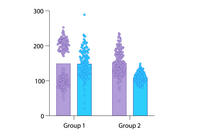
增强的分组图
轻松创建同时显示单个点(散点)、均值(或中值)线和误差线的图表。
更有效、更高效的研究
更开放的可访问文件的格式
通过使用行业标准格式(CSV、PNG、JSON等),您可以确保您的项目可以在Prism之外使用,并为您的数据工作流程和集成开辟新的可能性。
扩展的数据表功能
您可以根据需要打开任意多个窗口,数据最多可分为2048列,每个列中有512个子列。扩展的分析常量对话框允许您链接到所有类型分析的更多结果。
更智能的整理数据
全新升级的一系列工具,可帮助您准备数据进行分析。覆盖多变量数据表,选择和转换分析,提取和重新排列功能。
Hook常量对话框升级
在Prism中建立不同元素之间连接的方便方法。一个新的易于导航的树状结构现在覆盖了整个Prism分析库。
Prism提供了八种数据表
XY表
当每个数据点由单个X和Y值定义时使用。这类数据通常用线性或非线性回归模型拟合。
列表
用于通过单个分组变量组织成组的数据(例如,治疗组与对照组或女性与男性)。通常使用t检验和单因素方差分析。
分组表
用于按两个分组变量组织成组的数据(例如,女性对照组vs女性治疗组vs男性对照组vs男性治疗组)。通常使用双向方差分析。
列联表
用于按两个分组变量(治疗组与对照组、阳性结果与阴性结果)分组的计数数据。适合卡方检验和费雪精确检验。
生存表
用于Kaplan-Meier生存分析。每行代表一个受试者或个人,其中包含已经过的生存时间和结果。
整体分解
在有意义的情况下使用:“表中每个值占总数的百分比是多少?”用于计算分数和生成饼状图。
多变量表
当数据的每一行是不同的观测值,每一列是不同的变量并支持文本值时使用。可以直接用多元线性回归、Cox回归等进行分析,也可以重组为Prism的其他表类型之一。
嵌套表
当数据被组织成层次结构组时使用。使用嵌套t检验或嵌套单因素方差分析。
更复杂的统计分析
即使数据丢失,也可进行重复测量方差分析
现在,Prism 将自动拟合混合效果模型以完成此分析。
执行一元和多元逻辑回归
基于一个预测变量(一元逻辑回归)或多个预测变量(多元逻辑回归),将模型拟合为二进制结果(是/否、获胜/失败、通过/未通过)。
主成分分析(PCA)
计算并选择描述数据中最大方差的主成分。从选择技术中进行选择,包括通过蒙特卡罗模拟的并行分析、特征值阈值、方差比例阈值等。
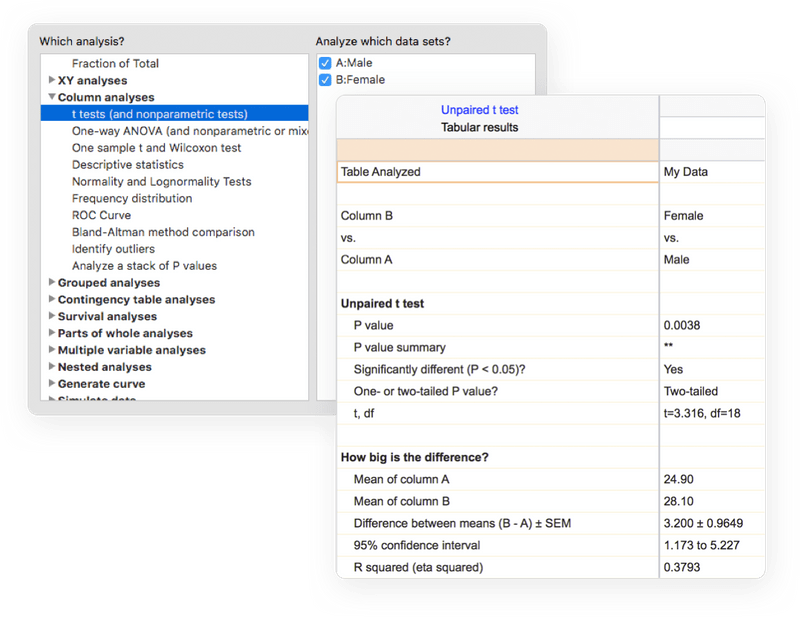
多重t检验(和非参数)分析
同时执行多个独立的双样本比较测试。从参数/非参数测试中进行选择,并指定数据是未配对的还是成对的。
在多元线性和多元逻辑回归中分析带有文本的分类变量
不需要编码!Prism支持自动编码分类变量并执行分析。指定引用并在模型中组织所有级别的分类变量,以获得清晰、可读的结果。
多元线性和多元逻辑回归的插值
使用指定的模型根据数据表中的数据或使用分析中指定的理论值来预测因变量的值。
发掘GraphPad Prism中可用统计特征的多样性
统计比较
- 配对或非配对 t 检验。 报告 P 值和置信区间。
- 通过多重t检验分析自动生成火山图(注意与P值的不同)。
- 非参数 Mann-Whitney 检验,包括中位数差值的置信区间。
- 用于比较两组的 Kolmogorov-Smirnov 检验。
- 含中位数置信区间的 Wilcoxon 检验。
- 一次执行多个 t 检验,使用错误发现率(或 Bonferroni 多重比较)选择哪些比较是需要进一步研究的新发现。
- 进行普通或重复测量方差分析,然后进行 Tukey、Newman-Keuls、Dunnett、Bonferroni 或 Holm-Sidak 多重比较检验,趋势后验或 Fisher 最小显著性检验。
- 在不假设群体具有相同标准偏差的情况下,使用 Brown-Forsythe 和 Welch 方差分析进行单因素方差分析,然后进行适当的比较检验(Games-Howell、Tamhane T2、Dunnett T3)
- 许多多重比较测试都伴随着置信区间和多重性调整的P值。
- 进行 Greenhouse-Geisser 校正,因此重复测量的单向、双向和三向方差分析不必假设结果呈球形分布。 选择此项时,多个比较检验也不必假设呈球形分布。
- 含 Dunn 后验的 Kruskal-Wallis 或 Friedman 非参数单向方差分析。
- Fisher 精确检验或卡方检验。 计算含置信区间的相对风险和优势比。
- 对即使在某些后验中仍缺少数值的数据进行双向方差分析。
- 对一个或两个因素进行重复测量的数据进行双向方差分析。 Tukey、Newman-Keuls、Dunnett、Bonferroni、Holm-Sidak 或 Fisher LSD 多重比较检验主要和简单效应。
- 三向方差分析(限制在其中两个因素中的两个级别,和在第三个因素中的任意数量的级别)。
- 使用混合效应模型(类似于重复测量方差分析,但能够处理丢失的数据),分析重复测量数据(单向、双向和三向)。
- Kaplan-Meier 生存分析。 应用对数秩检验(包括趋势检验)比较曲线。
- 使用嵌套 t 检验或嵌套单向方差分析比较嵌套数据表中的数据(使用混合效应模型)。
非线性回归
- 拟合我们的 105 个内置方程式之一,或输入您自己的方程式。 现在包括生长方程族: 指数生长、指数平台、Gompertz、Logistic 和 beta(先增长后衰减)。
- 输入微分或隐式方程。
- 输入用于不同数据集的方程。
- 全局非线性回归 – 在数据集之间共享参数。
- 强大的非线性回归功能。
- 自动识别或消除离群值。
- 使用额外的平方和 F 检验或 AICc 比较模型。
- 比较数据集之间的参数。
- 应用约束。
- 通过几种方法差分权重,并评估加权方法的效果。
- 接受自动初始估计值或输入您自己的值。
- 在指定的X值范围内自动绘制曲线图。
- 使用参数 SE 或 CI 量化拟合精度。 置信区间可为对称性(传统上)或不对称性(更准确)。
- 应用 Hougaard 偏度量化不精确的对称性。
- 绘制置信度或预测带。
- 检验残差的正态性。
- 运行或复制模型充分性检验。
- 报告协方差矩阵或依赖集。
- 从最佳拟合曲线中轻松插入数据点。
- 将直线拟合到两个数据集,并确定交点和双方斜率。
主成分分析Principal Component Analysis (PCA)
- 通过并行分析(Monte Carlo模拟)、Kaiser标准(特征值阈值)、方差阈值的比例等来选择主成分。
- 自动生成陡坡图、载荷图、双标图等
- 将PCA的分析结果用在Prism支持的主程序回归等分析中
多变量绘图Multiple Variable Graphing
- 指定定义轴坐标、颜色及尺寸的变量
- 创建气泡图
列统计
- 计算描述性统计: 最小值、最大值、四分位数、均值、标准差(SD)、标准误(SEM)、置信区间(CI)、变异系数(CV)、偏度、峰度。
- 含置信区间的均值或几何均值。
- 频率分布(从 bin 到直方图),包括累积直方图。
- 通过四种方法进行正态性检验(新功能: Anderson-Darling)。
- 对数正态性检验,以及从正态(高斯)与对数正态分布中取样的可能性。
- 创建 QQ 图作为正态性检验的一部分。
- 单样本 t 检验或 Wilcoxon 检验,用于对柱均值(或中位数)和理论值进行比较。
- 使用 Grubbs 或 ROUT 方法鉴别异常值。
- 分析批量 P 值,应用 Bonferroni 多重比较或 FDR 方法识别“重大”研究结果或发现。
简易的线性回归和相关性
- 计算含置信区间的斜率和截距。
- 强制回归线穿过指定点。
- 拟合以复制 Y 值或均值 Y。
- 应用运行测试来检验线性度偏离。
- 用四种不同方式(包括 QQ 图)计算和绘制残差图。
- 比较两条或更多条回归线的斜率和截距。
- 沿标准曲线插入新点。
- Pearson 或 Spearman(非参数)相关性。
广义线性模型(GLM)
- 使用新的多变量数据表生成多个自变量与单个因变量的相关模型。
- 多元线性回归(当Y连续时)。
- 泊松回归(当Y计数时;0,1,2,...)
- 逻辑回归(当Y为二进制时;是/否、通过/失败等)。
临床(诊断)实验室统计
- Bland-Altman 图。
- 受试者工作特征(ROC)曲线。
- Deming 回归(II 型线性回归)。
模拟
- 模拟XY、列或列联表。
- 重复模拟数据的分析,作为 Monte-Carlo 分析。
- 根据选择或输入的方程式和您选择的参数值绘制函数图。
其他计算
- 曲线下面积,含置信区间。
- 转换数据。
- 标准化。
- 鉴别异常值。
- 正态性检验。
- 转置表格。
- 减去基线(以及合并列)。
- 将每个值计算为其行、列或总计的分数。
联系我们&询价
Prism在Mac和Windows上可用。






 危险品化学品经营许可证(不带存储) 许可证编号:沪(杨)应急管危经许[2022]202944(QY)
危险品化学品经营许可证(不带存储) 许可证编号:沪(杨)应急管危经许[2022]202944(QY)  营业执照(三证合一)
营业执照(三证合一)